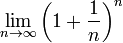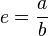LAS INTEGRALES

Las integrales, al igual que las derivadas anteriormente explicadas, son un concepto fundamental de las matemátic as avanzadas, especialmente en los campos del cálculo y del análisis matemático.

Una integral es, básicamente, la suma de los infinitos sumandos de una región determinada. Es el proceso inverso a las derivadas.

Los principales objetivos de las integrales son los siguientes:

• Cálculo del área de una región plana
• Volumen de un sólido de revolución
• Cambios de variables

 Existen diferentes tipos de resolver las integrales:

• Mediante cambios de variables: una parte de f(x) se sustituye por una variable t que simplifique la integral
• Racionales: si el denominador se puede descomponer en diferentes miembros en diferentes ecuaciones de grado 1: 

                              A/(x+t1)=B/(x+t2)=C/(x+t3)

• Por partes: 

                    


INTEGRALES INMEDIATAS:

LAS DERIVADAS

En la rama de cálculo de las matemáticas, las derivadas representan cómo una función cambia (y) a medida que su entrada (x) cambia.
Para funciones de valores reales de una sola variable, la derivada en un punto representa el valor de la pendiente de la recta tangente a la gráfica de la función en dicho punto.
El proceso de hallar una derivada se denomina diferenciación. El proceso fundamental del cálculo dice que la diferenciación es el proceso inverso a la integración en funciones continuas.

DERIVABILIDAD:

Una función con dominio dentro de los números reales, es derivable siempre y cuando se cumplan la siguiente condición:

• Tiene que se continua en el punto. Esto no quiere decir que siempre que sea continua una función, sea derivable. 
• Para que sea derivable, la pendiente debe ser igual a la izquierda y a la derecha del punto, es decir, que no tengas "picos".

INTERPRETACIÓN GEOMÉTRICA:

EL NÚMERO DE ORO EN LA NATURALEZA

Hemos hablado de la importancia del número de oro en la historia del arte. Ahora vamos a hablar de las manifestaciones de este número en la naturaleza.



En primer lugar, vamos a hablar de las espirales que forman los cuerpos de algunos seres vivos, por ejemplo, los caracoles:

A primera vista, quizá no veamos por ningún lado la proporción áurea. Sin embargo, si dividimos la imagen en rectángulos (quedándonos solo con la espiral, sin la imagen del caracol), queda de la siguiente manera:

En la imagen observamos muchos rectángulos áureos, que ya explicamos anteriormente. Si unimos, mediante una línea en espiral, como vemos en la fotografía, obtenemos lo que se llama espiral áurea.
 
 

Hemos hablado de la importancia del número de oro en la historia del arte. Ahora vamos a hablar de las manifestaciones de este número en la naturaleza.


Esta imagen de una piña también ofrece algunas espirales áureas.

Encontramos, en otros ámbitos de la naturaleza, fenómenos igual de sorprendentes que el anterior. El siguiente ejemplo, que trata sobre plantas, está relacionado con la sucesión de Fibonacci: si tomamos una hoja y vamos girando alrededor del tallo, contando las hojas, hasta encontrar otra con la misma orientación, el número de hojas “n” que hemos contado suele pertenecer a la sucesión de Fibonacci.



Algo igual de sorprendente es que, para llegar a encontrar una hoja con la misma orientación que otra elegida al azar, hay que dar al tallo un número “m” de vueltas completas, que también suele pertenecer a la sucesión de Fibonacci.



De hecho, al cociente m/n se le conoce como divergencia del tallo.



Otra relación entre las plantas y el número de oro es el número de pétalos que algunas de ellas suelen tener en sus flores. Este número de hojas suele pertenecer también a la sucesión de Fibonacci. Ahí van algunos ejemplos de esto:



Los lirios suelen tener 3 pétalos:

Los girasoles suelen tener 13, 21, 34, 55 o 89 pétalos:

ARTE Y MATEMÁTICAS EN LA ITALIA DE LEONARDO DA VINCI:

Seguimos estudiando la relación entre matemáticas y arte que ha venido apareciendo a lo largo de la historia. Si antes nos detuvimos en Grecia, ahora lo haremos en la Italia renacentista.




En esta época se produce un intento de regresar a la cultura y al arte clásicos, lo que hace que las obras de estos años se caractericen por su claridad y por su racionalidad. Esta última característica implica a las matemáticas. También aparece el antropocentrismo, las obras se centran en el hombre.



Empezaremos fijándonos en el hombre de Vitrubio, obra de Leonardo da Vinci que cumple todo lo expuesto anteriormente.



Una fotografía de la obra es la siguiente:







Como sabemos, Leonardo da Vinci fue uno de los personajes más inteligentes que pisaron la Tierra. Esta representación, como no podía ser de otra manera, guarda grandes relaciones entre sus partes que tienen que ver con el número de oro. Veamos algunas de ellas:

Aparte de las igualdades de la fotografía, muchas relaciones entre articulaciones de la imagen mantienen una relación áurea. Por ejemplo, 9/8 (codo-muñeca / muñeca-mano) = Ф , 12/11 (brazo / codo-mano) = Ф. También ocurre lo mismo con 17/16 , 14/13 , 2/1 , 2/3 , 5/4 , 6/5 y 7/6.



Por otra parte, Leonardo da Vinci también utilizó la proporción áurea en su famosa obra, la Mona Lisa. Lo vemos en la siguiente imagen:

Aunque sea difícil de creer, Leonardo da Vinci consiguió crear belleza con la proporción áurea, todos los rectángulos de la figura tienen una proporción áurea, hechos siguiendo paso a paso el método que exponemos.

 

Está claro que este tío fue un genio, ¿os dais cuenta de lo que hizo? ¡Creó arte usando solo un número y un rectángulo cuyos lados dan ese número como cociente!

Con razón dicen que fue el más inteligente de toda la historia.

LAS MATEMÁTICAS EN EL ARTE: LA ÉPOCA CLÁSICA

A lo largo de la historia, las matemáticas han jugado un papel fundamental en el arte de las diferentes culturas y civilizaciones, como veremos en los siguientes ejemplos.



El primer ejemplo que vamos a mostrar es el de la importancia del número de oro y la proporción áurea en la época clásica.



La siguiente imagen es una fotografía del Partenón, construido en el siglo V a.C. en Atenas.

Para los griegos, las matemáticas eran sinónimo de la armonía y de la belleza, incluso de la purificación del alma. Esto explica la siguiente relación matemática que encontramos en el Partenón:

 

Vemos que el Partenón podemos verlo como un gran rectángulo, cuya anchura es mayor que su altura. Si dividimos la anchura de este rectángulo entre su altura, obtenemos el número áureo, por lo que decimos que el rectángulo tiene una proporción áurea. Esta proporción está presente también en muchos otros cocientes de las medidas de los segmentos indicados en la figura. También vemos que el Partenón puede dividirse en seis rectángulos del mismo área, dos “horizontales” y cuatro “verticales”.

En el Partenón, además de en algunas relaciones entre segmentos y áreas, encontramos el número áureo en forma de rectángulos áureos, que son un ejemplo de la proporción áurea. Esto lo vemos en la siguiente fotografía:

 

Los rectángulos señalados en la fotografía son áureos. Este tipo de rectángulo se construye, geométricamente de la siguiente forma:

La explicación matemática de que al dividir las dimensiones del rectángulo obtengamos el número de oro es la siguiente: en el cuadrado de la izquierda vemos que la medida del segmento inferior es 1 + √5 , ya que en la parte derecha del cuadrado observamos una diagonal cuya medida es la raíz cuadrada de 2 al cuadrado más 1 al cuadrado, es decir, la raíz de 5. Si llevamos esta medida a la horizontal y sumamos 1, tal como se ve en la imagen, obtenemos 1 + √5.

Si el otro lado del rectángulo mide 2 unidades, entonces al dividir ambos lados nos quedará:

(1 + √5) / 2 , que es el número de oro.

SUCESIÓN DE FIBONACCI

La sucesión de Fibonacci es una sucesión de números naturales cuyos 10 primeros términos son los siguientes:




1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 600.



Como ves, en esta sucesión un término cualquiera es igual a la suma de los dos términos anteriores a él. Ahora vamos a comprobar una característica de esta sucesión. Para ello, primero divide dos términos consecutivos que no estén entre los tres primeros. Vuelve a dividir otros dos términos consecutivos.



Algunos resultados posibles son los siguientes:



1,5 , 1,667 , 1,6 , 1,625 , 1,615 , 1,619 , … , 1,618 , 1,59.



¿Qué observas?



Siempre obtenemos aproximadamente el mismo valor. ¿Te suena de algo este número?



Si recuerdas, los valores obtenidos están cada vez más cerca del número áureo, ф, cuya expresión era la siguiente:



ф = (1 + √5) / 2 .



Este valor es aproximadamente igual a 1,618.



Ahora proponemos un problema para aplicar esta sucesión:



En un bosque hay una especie de conejos cuyos individuos tardan 2 meses en estar preparados para dar a luz a nuevos individuos, y cuando están preparados para dar a luz a nuevos individuos paren a un macho y a una hembra por mes durante todos los meses, hasta que se mueren (estos conejos viven muchos años). Si en un momento determinado se aísla a una sola pareja de conejos de esta especie, ¿cuál será el número de parejas de conejos que habrá en cada mes trascurrido desde entonces?



En el primer mes y en el segundo, a la pareja no le da tiempo a dar a luz a nuevos conejos, por lo que solo habrá 1 pareja.



En el tercer mes, esa pareja dará a luz a otra pareja, por lo que habrá 2 parejas.



En el cuarto mes, la primera pareja dará a luz a una nueva pareja, pero la pareja que nació en el tercer mes aún no puede reproducirse.



En el quinto mes, la primera pareja y la que nació en el tercer mes se reproducen, por lo que aparecen 5 parejas en total.



Las parejas que hay en los sucesivos meses son:



1 , 1 , 2 , 3 , 5



Si te fijas, estos son los primeros términos de la sucesión de Fibonacci. Si continuamos desarrollando el problema, veremos que la sucesión de Fibonacci sigue adaptándose a la situación.



Este típico problema es uno de los ejemplos de las aplicaciones de la sucesión de Fibonacci.

EL NÚMERO "e"

El número e es una constante matemática que, al igual que π, es uno de los más importantes utilizados en las matemáticas y sus derivadas, como geometría o análisis complejo. Además es un número trascendente, es decir, que no se puede obtener mediante la resolución de una ecuación matemática. Su valor aproximado es:
                      e ≈ 2,71828...
   
Este número también es conocido, a veces, como el número de Euler o constante de Napier. Éste último, John Napier, fue quien introdujo por primera vez el concepto de logaritmo en el cálculo matemático.
   
La función e^x  tiene como particularidad que su derivada coincide con la misma función, lo que hace de ella que esta función exponencial se encuentre frecuentemente en el resultado de ecuaciones diferenciales sencillas. 


Por ello, es una constante importante en física, ya que hay varias leyes sencillas naturales que se rigen por él, como por ejemplo en vaciado de un depósito de agua. De esta misma forma, aparece en muchos otros ámbitos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos, biólogos, químicos, etc.


^{El descubrimiento de la constante se le acreditó a Jacob Bernoulli. Lo descubrió mediante un problema particular del llamado interés compuesto.} Al final de este problema, llegó a la siguiente conclusión, que da como resultado el valor del número e:

En matemáticas, la representación en serie del número e puede ser usado para probar que e es un número irracional.

DEMOSTRACIÓN:

Esta forma de demostrarlo, es una prueba por contradicción. Al principio, e es asumido como un número racional de la forma a/b.

Primeramente, se define el número de la siguiente forma:

En esta fórmula, x es un número entero que sustituye a e=a/b para así obtener:

<sup>Como el primer término es un entero, y cada fracción es la suma de un entero, x tiene que ser un entero también.


Ahora, la demostración consiste en probar que 0 < x < 1. Para ello insertaremos la serie representación de e en la definición de x para obtener: 





Para cualquier término con n < b + 1, obtenemos:</sup>







Si en esta fórmula cambiamos el índice de la sumatoria a k= n - b y usando la fórmula para a serie geométrica infinita, tenemos que:







Finalmente, vemos que como no hay ningún entero entre 0 y 1, hemos llegado a una contradicción, por lo que e tiene que ser irracional. 

EL NÚMERO π

El número π es un número irracional y una de las constantes más importantes usadas en matemáticas, física e ingeniería. Tiene un valor aproximado (truncado) de 3,14. Pi (π) establece la relación entre la longitud de la circunferencia y su diámetro. Anteriormente a este nombre, se le llamó constante de Arquímedes.


A lo largo de la historia, el número π ha sido objeto de numerosos matemáticos para determinar el valor de dicho númer. Algunas de las aproximaciones históricas realizadas son las que vamos a comentar:

• EGIPTO: llevada a cabo por el egipcio Ahmes en el 1800 a.C. Según afirmaba, "el área del círculo es aproximadamente igual a la de un cuadrado de lado igual a 8/9 del diámetro del círculo".

                                      π= (8/9 d)² = 64/81 d² = 64/81 (4r²) = 256/81 = 3,16049...

• MESOPOTAMIA: los matemáticos mesopotámicos empleaban para el cálculo de segmentos un valor de π igual a 3 + 1/8

• MATEMÁTICA CHINA:  hacia el año 263, el matemático chino Liu Hui fue el primero en sugerir que 3,14 era una buena aproximación para π. Para descubrirlo, utilizó poligonos de 96 y 192 lados respectivamente. Posteriormente, estimó un valor de π igual a 3,14159 utilizando un políogono de 3.072 lados.

A pesar de ser un número irracional, es uno de los números más usados sobre todo en las siguientes materias: geometría, probabilidad, análisis matemático....


CURIOSIDADES DEL NÚMERO PI:

Para recordar las 20 primeras cifras del número π existe un poema, que contando las letras de cada palabra, coincide con los dígitos del número:

Soy y seré a todos definible
mi nombre tengo que daros
cociente diametral siempre inmedible
soy de los redondos aros 

PARADOJAS DE ZENÓN DE ELEA

Las paradojas de Zenón de Elea son una serie de aporías para apoyar la doctrina de Parménides de que las sensaciones no son más que ilusiones, y con lo que intenta explicar que no existe el movimiento.
Las tres paradojas más conocidas de este filósofo griego son las siguientes:

AQUILES Y LA TORTUGA:
 Aquiles, un gran guerrero llamado el "pies ligero" decide salir a competir en una carrera contra una tortuga. Ya que corre mucho más rápido que la tortuga y seguro de sus posibilidades, le cede una gran ventaja inicial. Al darse la salida, Aquiles recorre la distancia que les separaba rápidamente, pero al llegar se da cuenta de que la tortuga no está ahí, sino que ha avanzado. Sigue corriendo, pero al llegar de nuevo a donde estaba la tortuga, ésta ha vuelto a avanzar.
Según lo anteriormente dicho, Aquiles no podrá ganar nunca la carrera, ya que para alcanzar a la tortuga, tendrá que recorrer un número infinito de puntos antes de alcanzarla.

LA DICOTOMÍA:
Esta paradoja es muy parecida a la anterior. Zenón se encuentra a ocho metros de un árbol. Llegado un momento, lanza una piedra, tratando de dar al árbol. La piedra antes de llegar al objetivo, primero ha de recorrer la mitad de la distancia que lo separa, es decir, los cuatro primeros metros. Después deberá recorrer esos cuatro metros restantes, pero para ello, de nuevo deberá recorrer la mitad de esa distancia. Según esta regla, siempre deberá recorrer la mitad de la distancia, por lo que la piedra nunca llegará al árbol.


LA PARADOJA DE LA FLECHA:
 
En esta paradoja, se lanza una flecha. En cada momento, la flecha está en una posición específica, y si ese momento es o suficientemente pequeño, la flecha no tiene tiempo para moverse, por lo que está en reposo durante ese instante. Ahora bien, durante los siguientes periodos de tiempo, la flecha también estará en reposo por el mismo motivo. De este modo, se puede llegar a la conclusión de que siempre está en reposo: el movimiento es imposible.



Estos son unos ejemplos, a través de los cuales Zenón intenta explicar que el movimiento físico no existe.

EL PRISIONERO DE LA HABITACIÓN DE FERMAT

En la película "La habitación de Fermat" aparecen varios acertijos, que tienen que ser resueltos por varios personajes que están atrapados en una habitación en la que, si no resuelven rápido los acertijos, morirán.

El acertijo consiste en lo siguiente: un prisionero está en una habitación con dos  puertas: una de ellas conduce a la libertad y otra a la muerte. Cada puerta está custodiada por un guardia. De los dos guardias, uno siempre dice la verdad y otro siempre miente. El prisionero no sabe cuál de los guardias es el que siempre dice la verdad y cuál es el que miente. Con una sola pregunta, tiene que descubrir cuál es la puerta que conduce a la libertad. ¿Cuál es la pregunta que debe hacer el prisionero?

Si preguntase, por ejemplo: "¿Qué puerta conduce a la libertad?, el prisionero no sabría cuál es la puerta buena, porque si el guardia al que le preguntara fuese el que siempre dice la verdad, la respuesta que le daría el guardia sería la correcta, pero si el guardia fuera el que miente, la respuesta sería falsa.

Solución:

El prisionero debe preguntar "¿Cuál es la puerta que el otro guardia, me indicaría como la puerta que me llevará a la libertad?". Si la pregunta se la ha hecho al mentiroso dirá: "mi compañero te indicará la puerta X", pero como es mentira, la puerta que debería elegir sería la que no es M. En cambio, si le hace la pregunta al guardián que no miente, te dirá la verdad, diciendo: "mi compañero te indicará la puerta X", y como el compañero sí miente, la puerta a elegir no será la puerta X.


En conclusión, el prisionero ha de elegir la puerta contraria a la que indique cualquiera de los dos terribles guardianes en su respuesta.

¿ERES TONTO?

Si en la entrada anterior habíamos hablado de imágenes quietas que engañaban a nuestros sentidos y parecían moverse, ahora hablaremos de imágenes o animaciones con movimiento que además de engañarnos nos hacen parecer tontos.

La primero que vamos a hacer es ver la siguiente animación.

Hay que mirar a la cruz negra y mantener fija la vista (intenta no parpadear) durante algún tiempo (20 o 30 segundos). No seas gandul, que sé yo que no tienes nada que hacer si estás aquí todavía.

¿Qué observas?

Al cabo de 10 - 15 segundos los puntos rosas desaparecen. Si aún sigues un tiempo, llegarás a alucinar, y verás lo siguiente:

Es increíble. ¿Qué explicación puede tener esto? Pues ya lo hemos dicho: las imágenes nos engañan y nos hacen parecer tontos.

Lo segundo que vamos a hacer es ver algunos vídeos sobre este tema:

VÍDEO 1:



VÍDEO 2:




VÍDEO 3:

IMÁGENES VIVAS

Tras haber analizado algunas imágenes inexplicables y otras de difícil solución, vamos a ver ahora algunas imágenes que provocan el fallo de nuestros sentidos.

La primera imagen es la siguiente:

La forma de actuar es la siguiente: mira el punto negro del centro fijamente y mueve la cabeza adelante y atrás sin apartar la vista de él.

¿Qué observas?

Parece que las circunferencias de alrededor se mueven, pero... ¿es cierto o es una ilusión?

Obviamente se trata de una ilusión óptica, debida, como hemos dicho al principio, a que las imágenes pueden engañar a nuestros sentidos.


La segunda imagen es la siguiente:

Tienes que hacer lo siguiente: mira fijamente uno de los cuatro círculos grandes.

¿Qué observas?

¡¡¡Los otros círculos se mueven!!!

Se trata de otra ilusión óptica, causada por la misma razón.

La tercera imagen es la siguiente:

¡¡¡Esta solo con mirarla ya parece que tiembla!!!

De nuevo, una imagen engaña nuestros sentidos.

Si te han gustado estas imágenes, mira la siguiente entrada.

TRIÁNGULO MISTERIOSO

Observa detalladamente las siguientes imágenes:

Obviamente, el área de una figura dividida en varias figuras es la suma del área de cada una de las figuras. Sin embargo, en esta imagen aparece de nuevo una incongruencia: si lo anterior es cierto, entonces el mismo triángulo debería tener un área de Arojo + Aazul + Aamarillo + Averde (arriba), mientras que abajo su área sería Arojo + Aazul + Aamarillo + Averde + 1. Está claro que algo no cuadra. Intenta explicar detalladamente esta situación (observa detenidamente la imagen, piensa que la cuadrícula está ahí para algo).





PISTA:

Te habrás dado cuenta de que el triángulo de arriba está más achatado y el de abajo está más inflado. Sabiendo esto, intenta explicar qué es lo que pasa (¡¡¡no seas gandul, que si estás viendo esto es porque no tienes nada que hacer!!!).







SOLUCIÓN:

La pendiente del triángulo azul (2/5) es ligeramente mayor que la del rojo (3/8). Por lo tanto, en la hipotenusa del "triángulo" grande (que no es realmente un triángulo) se produce un punto anguloso, en el que cambia la pendiente. Si el punto anguloso es saliente (abajo), hay una mayor área que si el punto anguloso es entrante (arriba). Esa diferencia de área es la que hay que rellenar abajo con un cuadrado en blanco.

Mira la imagen de abajo:

Hay otras situaciones que requieren del uso de la lógica para ser resueltas. En la imagen de abajo apreciamos un puzle en el que hay que cuadrar todas las piezas para que ninguna se quede fuera.

¿Te parece imposible? Pues yo creo que con todo lo que llevamos visto en este blog...

MÁS JUEGOS CON CARAS

Seguimos en la línea de imágenes inexplicables para nuestra inteligencia. Esta vez vamos a proponer unas cuantas imágenes de caras que esconden algún secreto. Va a ser difícil descubrir todos los secretos, pero vamos a intentarlo al menos.

Empecemos con la siguiente imagen:

En ella observamos, en primer lugar una cara de un hombre mayor, la parte superior de su vestimenta y su mano en el pecho.

Sin embargo, si miramos detalladamente, vemos que hay diversas imágenes (de personas y animales) integradas en la cara del anciano. Hay algunas que son fáciles de ver, pero otras no lo son tanto.





PISTA:

Las figuras que forman el ojo, la oreja y la mano del anciano son muy fáciles de adivinar.
Hay otras cinco. Cuatro de ellas están concentradas en la zona superior izquierda de la imagen. Venga, busca un poco más y luego miras la solución.





SOLUCIÓN:

1) Cara de frente en el cielo.


2) Cara de perfil en el cielo.

3) Cara de perfil en el cielo.

4) Cara de perfil en el cielo.

5) Cara de perfil en el cielo.

Las últimas cuatro caras están formadas por el contraste entre la figura principal de la imagen y el fondo, siguiendo el ejemplo de la siguiente imagen famosa:

6) Señora de falda larga.

7) Niño en brazos de esta señora.

8) Anciano con sombrero y barba blanca.

El número 9 se refiere a la figura general, a la cara del anciano.

Hay muchas imágenes similares:

CAMBIOS DE HUMOR REPENTINOS

Continuamos con el ámbito de aquello que se escapa a la lógica. Esta vez vamos a observar un efecto óptico explicable pero, aun así, impresionante.

En primer lugar, vamos a observar la imagen de más abajo a una distancia de 20 cm de la pantalla del ordenador. Después nos iremos alejando progresivamente de ella hasta alejarnos 2 metros del ordenador. Es importante que no seas un gandul y que te levantes de la silla!!! Si no lo haces y piensas que esto es una chorrada, no funcionará el experimento.

La imagen es la siguiente.

Observa que la cara de la izquierda es "desagradable" mientras que la de la derecha es "agradable".

Ahora levántate (¡¡¡que no seas gandul!!!) y, sin dejar de mirar la pantalla, retrocede hasta dos metros.

¿Qué observas?

¡¡¡Las caras han cambiado de sitio!!!

Este efecto, creado por Phillipe Schyns, se basa en la alternancia entre luces y sombras. Conforme nos alejamos, la proporción luz-sombra que vamos percibiendo va cambiando. Esa es la razón del cambio del estado de ánimo de las caras.

Al margen de este efecto espectacular, hay otras imágenes que "juegan" con caras. Ahí van algunos ejemplos:

¿Músico o mujer?