Las paradojas de Zenón de Elea son una serie de aporías para apoyar la doctrina de Parménides de que las sensaciones no son más que ilusiones, y con lo que intenta explicar que no existe el movimiento.
Las tres paradojas más conocidas de este filósofo griego son las siguientes:
AQUILES Y LA TORTUGA:
Aquiles, un gran guerrero llamado el "pies ligero" decide salir a competir en una carrera contra una tortuga. Ya que corre mucho más rápido que la tortuga y seguro de sus posibilidades, le cede una gran ventaja inicial. Al darse la salida, Aquiles recorre la distancia que les separaba rápidamente, pero al llegar se da cuenta de que la tortuga no está ahí, sino que ha avanzado. Sigue corriendo, pero al llegar de nuevo a donde estaba la tortuga, ésta ha vuelto a avanzar.
Según lo anteriormente dicho, Aquiles no podrá ganar nunca la carrera, ya que para alcanzar a la tortuga, tendrá que recorrer un número infinito de puntos antes de alcanzarla.
LA DICOTOMÍA:
Esta paradoja es muy parecida a la anterior. Zenón se encuentra a ocho metros de un árbol. Llegado un momento, lanza una piedra, tratando de dar al árbol. La piedra antes de llegar al objetivo, primero ha de recorrer la mitad de la distancia que lo separa, es decir, los cuatro primeros metros. Después deberá recorrer esos cuatro metros restantes, pero para ello, de nuevo deberá recorrer la mitad de esa distancia. Según esta regla, siempre deberá recorrer la mitad de la distancia, por lo que la piedra nunca llegará al árbol.
LA PARADOJA DE LA FLECHA:
En esta paradoja, se lanza una flecha. En cada momento, la flecha está en una posición específica, y si ese momento es o suficientemente pequeño, la flecha no tiene tiempo para moverse, por lo que está en reposo durante ese instante. Ahora bien, durante los siguientes periodos de tiempo, la flecha también estará en reposo por el mismo motivo. De este modo, se puede llegar a la conclusión de que siempre está en reposo: el movimiento es imposible.
Estos son unos ejemplos, a través de los cuales Zenón intenta explicar que el movimiento físico no existe.
15 feb 2011
29 ene 2011
EL PRISIONERO DE LA HABITACIÓN DE FERMAT
En la película "La habitación de Fermat" aparecen varios acertijos, que tienen que ser resueltos por varios personajes que están atrapados en una habitación en la que, si no resuelven rápido los acertijos, morirán.
El acertijo consiste en lo siguiente: un prisionero está en una habitación con dos puertas: una de ellas conduce a la libertad y otra a la muerte. Cada puerta está custodiada por un guardia. De los dos guardias, uno siempre dice la verdad y otro siempre miente. El prisionero no sabe cuál de los guardias es el que siempre dice la verdad y cuál es el que miente. Con una sola pregunta, tiene que descubrir cuál es la puerta que conduce a la libertad. ¿Cuál es la pregunta que debe hacer el prisionero?
Si preguntase, por ejemplo: "¿Qué puerta conduce a la libertad?, el prisionero no sabría cuál es la puerta buena, porque si el guardia al que le preguntara fuese el que siempre dice la verdad, la respuesta que le daría el guardia sería la correcta, pero si el guardia fuera el que miente, la respuesta sería falsa.
El prisionero debe preguntar "¿Cuál es la puerta que el otro guardia, me indicaría como la puerta que me llevará a la libertad?". Si la pregunta se la ha hecho al mentiroso dirá: "mi compañero te indicará la puerta X", pero como es mentira, la puerta que debería elegir sería la que no es M. En cambio, si le hace la pregunta al guardián que no miente, te dirá la verdad, diciendo: "mi compañero te indicará la puerta X", y como el compañero sí miente, la puerta a elegir no será la puerta X.
En conclusión, el prisionero ha de elegir la puerta contraria a la que indique cualquiera de los dos terribles guardianes en su respuesta.
El acertijo consiste en lo siguiente: un prisionero está en una habitación con dos puertas: una de ellas conduce a la libertad y otra a la muerte. Cada puerta está custodiada por un guardia. De los dos guardias, uno siempre dice la verdad y otro siempre miente. El prisionero no sabe cuál de los guardias es el que siempre dice la verdad y cuál es el que miente. Con una sola pregunta, tiene que descubrir cuál es la puerta que conduce a la libertad. ¿Cuál es la pregunta que debe hacer el prisionero?
Si preguntase, por ejemplo: "¿Qué puerta conduce a la libertad?, el prisionero no sabría cuál es la puerta buena, porque si el guardia al que le preguntara fuese el que siempre dice la verdad, la respuesta que le daría el guardia sería la correcta, pero si el guardia fuera el que miente, la respuesta sería falsa.
Solución:
En conclusión, el prisionero ha de elegir la puerta contraria a la que indique cualquiera de los dos terribles guardianes en su respuesta.
25 ene 2011
¿ERES TONTO?
Si en la entrada anterior habíamos hablado de imágenes quietas que engañaban a nuestros sentidos y parecían moverse, ahora hablaremos de imágenes o animaciones con movimiento que además de engañarnos nos hacen parecer tontos.
La primero que vamos a hacer es ver la siguiente animación.
La primero que vamos a hacer es ver la siguiente animación.
Hay que mirar a la cruz negra y mantener fija la vista (intenta no parpadear) durante algún tiempo (20 o 30 segundos). No seas gandul, que sé yo que no tienes nada que hacer si estás aquí todavía.
¿Qué observas?
Al cabo de 10 - 15 segundos los puntos rosas desaparecen. Si aún sigues un tiempo, llegarás a alucinar, y verás lo siguiente:
Es increíble. ¿Qué explicación puede tener esto? Pues ya lo hemos dicho: las imágenes nos engañan y nos hacen parecer tontos.
Lo segundo que vamos a hacer es ver algunos vídeos sobre este tema:
VÍDEO 1:
VÍDEO 2:
VÍDEO 3:
VÍDEO 1:
VÍDEO 2:
VÍDEO 3:
IMÁGENES VIVAS
Tras haber analizado algunas imágenes inexplicables y otras de difícil solución, vamos a ver ahora algunas imágenes que provocan el fallo de nuestros sentidos.
La primera imagen es la siguiente:

La forma de actuar es la siguiente: mira el punto negro del centro fijamente y mueve la cabeza adelante y atrás sin apartar la vista de él.
¿Qué observas?
Parece que las circunferencias de alrededor se mueven, pero... ¿es cierto o es una ilusión?
Obviamente se trata de una ilusión óptica, debida, como hemos dicho al principio, a que las imágenes pueden engañar a nuestros sentidos.
La segunda imagen es la siguiente:

La primera imagen es la siguiente:

La forma de actuar es la siguiente: mira el punto negro del centro fijamente y mueve la cabeza adelante y atrás sin apartar la vista de él.
¿Qué observas?
Parece que las circunferencias de alrededor se mueven, pero... ¿es cierto o es una ilusión?
Obviamente se trata de una ilusión óptica, debida, como hemos dicho al principio, a que las imágenes pueden engañar a nuestros sentidos.
La segunda imagen es la siguiente:
Tienes que hacer lo siguiente: mira fijamente uno de los cuatro círculos grandes.
¿Qué observas?
¡¡¡Los otros círculos se mueven!!!
Se trata de otra ilusión óptica, causada por la misma razón.
La tercera imagen es la siguiente:

¡¡¡Esta solo con mirarla ya parece que tiembla!!!
De nuevo, una imagen engaña nuestros sentidos.
Si te han gustado estas imágenes, mira la siguiente entrada.
TRIÁNGULO MISTERIOSO
Observa detalladamente las siguientes imágenes:
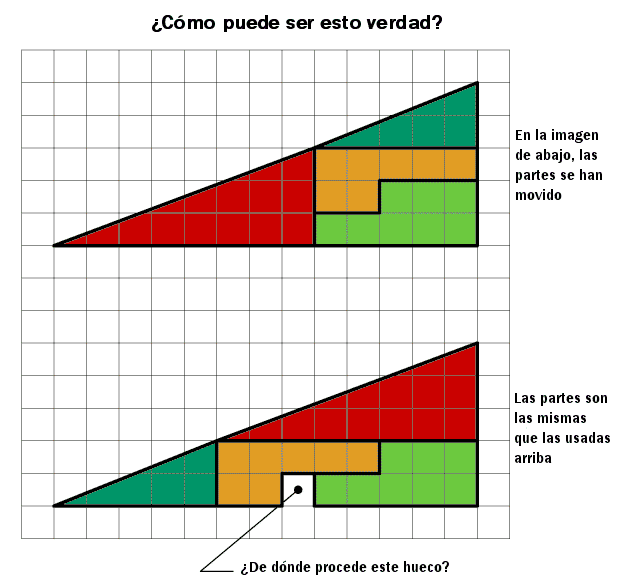
Obviamente, el área de una figura dividida en varias figuras es la suma del área de cada una de las figuras. Sin embargo, en esta imagen aparece de nuevo una incongruencia: si lo anterior es cierto, entonces el mismo triángulo debería tener un área de Arojo + Aazul + Aamarillo + Averde (arriba), mientras que abajo su área sería Arojo + Aazul + Aamarillo + Averde + 1. Está claro que algo no cuadra. Intenta explicar detalladamente esta situación (observa detenidamente la imagen, piensa que la cuadrícula está ahí para algo).
PISTA:
Te habrás dado cuenta de que el triángulo de arriba está más achatado y el de abajo está más inflado. Sabiendo esto, intenta explicar qué es lo que pasa (¡¡¡no seas gandul, que si estás viendo esto es porque no tienes nada que hacer!!!).
SOLUCIÓN:
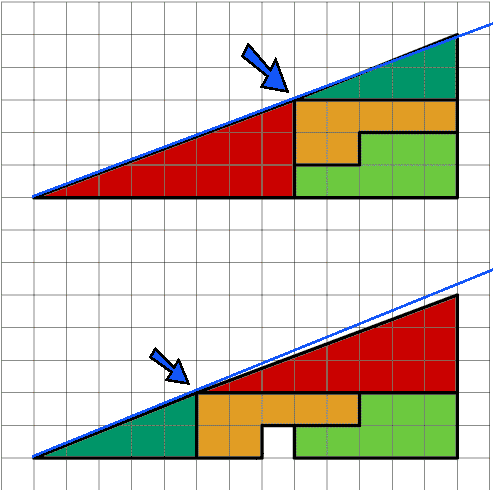
La pendiente del triángulo azul (2/5) es ligeramente mayor que la del rojo (3/8). Por lo tanto, en la hipotenusa del "triángulo" grande (que no es realmente un triángulo) se produce un punto anguloso, en el que cambia la pendiente. Si el punto anguloso es saliente (abajo), hay una mayor área que si el punto anguloso es entrante (arriba). Esa diferencia de área es la que hay que rellenar abajo con un cuadrado en blanco.
Mira la imagen de abajo:


Obviamente, el área de una figura dividida en varias figuras es la suma del área de cada una de las figuras. Sin embargo, en esta imagen aparece de nuevo una incongruencia: si lo anterior es cierto, entonces el mismo triángulo debería tener un área de Arojo + Aazul + Aamarillo + Averde (arriba), mientras que abajo su área sería Arojo + Aazul + Aamarillo + Averde + 1. Está claro que algo no cuadra. Intenta explicar detalladamente esta situación (observa detenidamente la imagen, piensa que la cuadrícula está ahí para algo).
PISTA:
Te habrás dado cuenta de que el triángulo de arriba está más achatado y el de abajo está más inflado. Sabiendo esto, intenta explicar qué es lo que pasa (¡¡¡no seas gandul, que si estás viendo esto es porque no tienes nada que hacer!!!).
SOLUCIÓN:
La pendiente del triángulo azul (2/5) es ligeramente mayor que la del rojo (3/8). Por lo tanto, en la hipotenusa del "triángulo" grande (que no es realmente un triángulo) se produce un punto anguloso, en el que cambia la pendiente. Si el punto anguloso es saliente (abajo), hay una mayor área que si el punto anguloso es entrante (arriba). Esa diferencia de área es la que hay que rellenar abajo con un cuadrado en blanco.
Mira la imagen de abajo:

Hay otras situaciones que requieren del uso de la lógica para ser resueltas. En la imagen de abajo apreciamos un puzle en el que hay que cuadrar todas las piezas para que ninguna se quede fuera.

¿Te parece imposible? Pues yo creo que con todo lo que llevamos visto en este blog...
Suscribirse a:
Entradas (Atom)



