25 mar 2011

EL NÚMERO "e"

El número e es una constante matemática que, al igual que π, es uno de los más importantes utilizados en las matemáticas y sus derivadas, como geometría o análisis complejo. Además es un número trascendente, es decir, que no se puede obtener mediante la resolución de una ecuación matemática. Su valor aproximado es:
                      e ≈ 2,71828...
   
Este número también es conocido, a veces, como el número de Euler o constante de Napier. Éste último, John Napier, fue quien introdujo por primera vez el concepto de logaritmo en el cálculo matemático.
   
La función ex  tiene como particularidad que su derivada coincide con la misma función, lo que hace de ella que esta función exponencial se encuentre frecuentemente en el resultado de ecuaciones diferenciales sencillas. 


Por ello, es una constante importante en física, ya que hay varias leyes sencillas naturales que se rigen por él, como por ejemplo en vaciado de un depósito de agua. De esta misma forma, aparece en muchos otros ámbitos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos, biólogos, químicos, etc.


El descubrimiento de la constante se le acreditó a Jacob Bernoulli. Lo descubrió mediante un problema particular del llamado interés compuesto. Al final de este problema, llegó a la siguiente conclusión, que da como resultado el valor del número e:

\lim_{n\to\infty} \left(1+{1\over n}\right)^n

En matemáticas, la representación en serie del número e puede ser usado para probar que e es un número irracional.

DEMOSTRACIÓN:
Esta forma de demostrarlo, es una prueba por contradicción. Al principio, e es asumido como un número racional de la forma a/b.
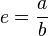
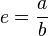
e = \frac{a}{b}
Primeramente, se define el número de la siguiente forma:
\ x = b!\,\biggl(e - \sum_{n = 0}^{b} \frac{1}{n!}\biggr).
En esta fórmula, x es un número entero que sustituye a e=a/b para así obtener:
x = b!\,\biggl(\frac{a}{b} - \sum_{n = 0}^{b} \frac{1}{n!}\biggr) = a(b - 1)! - \sum_{n = 0}^{b} \frac{b!}{n!}\,.


Como el primer término es un entero, y cada fracción es la suma de un entero, x tiene que ser un entero también.


Ahora, la demostración consiste en probar que 0 < x < 1. Para ello insertaremos la serie representación de e en la definición de x para obtener: 


x = \sum_{n = b+1}^{\infty} \frac{b!}{n!}>0\,.


Para cualquier término con n < b + 1, obtenemos:


\frac{b!}{n!} =\frac1{(b+1)(b+2)\cdots(b+(n-b))} \le\frac1{(b+1)^{n-b}}\,,




Si en esta fórmula cambiamos el índice de la sumatoria a k= n - b y usando la fórmula para a serie geométrica infinita, tenemos que:


x =\sum_{n = b+1}^{\infty} \frac{b!}{n!} < \sum_{k=1}^\infty\frac1{(b+1)^k} =\frac{1}{b+1}\biggl(\frac1{1-\frac1{b+1}}\biggr) = \frac{1}{b} \le 1.




Finalmente, vemos que como no hay ningún entero entre 0 y 1, hemos llegado a una contradicción, por lo que e tiene que ser irracional. 

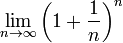
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)