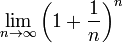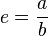28 mar 2011

LAS MATEMÁTICAS EN EL ARTE: LA ÉPOCA CLÁSICA

A lo largo de la historia, las matemáticas han jugado un papel fundamental en el arte de las diferentes culturas y civilizaciones, como veremos en los siguientes ejemplos.



El primer ejemplo que vamos a mostrar es el de la importancia del número de oro y la proporción áurea en la época clásica.



La siguiente imagen es una fotografía del Partenón, construido en el siglo V a.C. en Atenas.








Para los griegos, las matemáticas eran sinónimo de la armonía y de la belleza, incluso de la purificación del alma. Esto explica la siguiente relación matemática que encontramos en el Partenón:


 
Vemos que el Partenón podemos verlo como un gran rectángulo, cuya anchura es mayor que su altura. Si dividimos la anchura de este rectángulo entre su altura, obtenemos el número áureo, por lo que decimos que el rectángulo tiene una proporción áurea. Esta proporción está presente también en muchos otros cocientes de las medidas de los segmentos indicados en la figura. También vemos que el Partenón puede dividirse en seis rectángulos del mismo área, dos “horizontales” y cuatro “verticales”.



En el Partenón, además de en algunas relaciones entre segmentos y áreas, encontramos el número áureo en forma de rectángulos áureos, que son un ejemplo de la proporción áurea. Esto lo vemos en la siguiente fotografía:

 


Los rectángulos señalados en la fotografía son áureos. Este tipo de rectángulo se construye, geométricamente de la siguiente forma:




La explicación matemática de que al dividir las dimensiones del rectángulo obtengamos el número de oro es la siguiente: en el cuadrado de la izquierda vemos que la medida del segmento inferior es 1 + √5 , ya que en la parte derecha del cuadrado observamos una diagonal cuya medida es la raíz cuadrada de 2 al cuadrado más 1 al cuadrado, es decir, la raíz de 5. Si llevamos esta medida a la horizontal y sumamos 1, tal como se ve en la imagen, obtenemos 1 + √5.



Si el otro lado del rectángulo mide 2 unidades, entonces al dividir ambos lados nos quedará:



(1 + √5) / 2 , que es el número de oro.
No hay comentarios:

SUCESIÓN DE FIBONACCI

La sucesión de Fibonacci es una sucesión de números naturales cuyos 10 primeros términos son los siguientes:




1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 600.



Como ves, en esta sucesión un término cualquiera es igual a la suma de los dos términos anteriores a él. Ahora vamos a comprobar una característica de esta sucesión. Para ello, primero divide dos términos consecutivos que no estén entre los tres primeros. Vuelve a dividir otros dos términos consecutivos.



Algunos resultados posibles son los siguientes:



1,5 , 1,667 , 1,6 , 1,625 , 1,615 , 1,619 , … , 1,618 , 1,59.



¿Qué observas?



Siempre obtenemos aproximadamente el mismo valor. ¿Te suena de algo este número?



Si recuerdas, los valores obtenidos están cada vez más cerca del número áureo, ф, cuya expresión era la siguiente:



ф = (1 + √5) / 2 .



Este valor es aproximadamente igual a 1,618.



Ahora proponemos un problema para aplicar esta sucesión:



En un bosque hay una especie de conejos cuyos individuos tardan 2 meses en estar preparados para dar a luz a nuevos individuos, y cuando están preparados para dar a luz a nuevos individuos paren a un macho y a una hembra por mes durante todos los meses, hasta que se mueren (estos conejos viven muchos años). Si en un momento determinado se aísla a una sola pareja de conejos de esta especie, ¿cuál será el número de parejas de conejos que habrá en cada mes trascurrido desde entonces?



En el primer mes y en el segundo, a la pareja no le da tiempo a dar a luz a nuevos conejos, por lo que solo habrá 1 pareja.



En el tercer mes, esa pareja dará a luz a otra pareja, por lo que habrá 2 parejas.



En el cuarto mes, la primera pareja dará a luz a una nueva pareja, pero la pareja que nació en el tercer mes aún no puede reproducirse.



En el quinto mes, la primera pareja y la que nació en el tercer mes se reproducen, por lo que aparecen 5 parejas en total.



Las parejas que hay en los sucesivos meses son:



1 , 1 , 2 , 3 , 5



Si te fijas, estos son los primeros términos de la sucesión de Fibonacci. Si continuamos desarrollando el problema, veremos que la sucesión de Fibonacci sigue adaptándose a la situación.



Este típico problema es uno de los ejemplos de las aplicaciones de la sucesión de Fibonacci.




No hay comentarios:

25 mar 2011

EL NÚMERO "e"

El número e es una constante matemática que, al igual que π, es uno de los más importantes utilizados en las matemáticas y sus derivadas, como geometría o análisis complejo. Además es un número trascendente, es decir, que no se puede obtener mediante la resolución de una ecuación matemática. Su valor aproximado es:
                      e ≈ 2,71828...
   
Este número también es conocido, a veces, como el número de Euler o constante de Napier. Éste último, John Napier, fue quien introdujo por primera vez el concepto de logaritmo en el cálculo matemático.
   
La función ex  tiene como particularidad que su derivada coincide con la misma función, lo que hace de ella que esta función exponencial se encuentre frecuentemente en el resultado de ecuaciones diferenciales sencillas. 


Por ello, es una constante importante en física, ya que hay varias leyes sencillas naturales que se rigen por él, como por ejemplo en vaciado de un depósito de agua. De esta misma forma, aparece en muchos otros ámbitos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos, biólogos, químicos, etc.


El descubrimiento de la constante se le acreditó a Jacob Bernoulli. Lo descubrió mediante un problema particular del llamado interés compuesto. Al final de este problema, llegó a la siguiente conclusión, que da como resultado el valor del número e:

\lim_{n\to\infty} \left(1+{1\over n}\right)^n

En matemáticas, la representación en serie del número e puede ser usado para probar que e es un número irracional.

DEMOSTRACIÓN:
Esta forma de demostrarlo, es una prueba por contradicción. Al principio, e es asumido como un número racional de la forma a/b.
e = \frac{a}{b}
Primeramente, se define el número de la siguiente forma:
\ x = b!\,\biggl(e - \sum_{n = 0}^{b} \frac{1}{n!}\biggr).
En esta fórmula, x es un número entero que sustituye a e=a/b para así obtener:
x = b!\,\biggl(\frac{a}{b} - \sum_{n = 0}^{b} \frac{1}{n!}\biggr) = a(b - 1)! - \sum_{n = 0}^{b} \frac{b!}{n!}\,.


Como el primer término es un entero, y cada fracción es la suma de un entero, x tiene que ser un entero también.


Ahora, la demostración consiste en probar que 0 < x < 1. Para ello insertaremos la serie representación de e en la definición de x para obtener: 


x = \sum_{n = b+1}^{\infty} \frac{b!}{n!}>0\,.


Para cualquier término con n < b + 1, obtenemos:


\frac{b!}{n!} =\frac1{(b+1)(b+2)\cdots(b+(n-b))} \le\frac1{(b+1)^{n-b}}\,,




Si en esta fórmula cambiamos el índice de la sumatoria a k= n - b y usando la fórmula para a serie geométrica infinita, tenemos que:


x =\sum_{n = b+1}^{\infty} \frac{b!}{n!} < \sum_{k=1}^\infty\frac1{(b+1)^k} =\frac{1}{b+1}\biggl(\frac1{1-\frac1{b+1}}\biggr) = \frac{1}{b} \le 1.




Finalmente, vemos que como no hay ningún entero entre 0 y 1, hemos llegado a una contradicción, por lo que e tiene que ser irracional. 
No hay comentarios:

8 mar 2011

EL NÚMERO π

El número π es un número irracional y una de las constantes más importantes usadas en matemáticas, física e ingeniería. Tiene un valor aproximado (truncado) de 3,14. Pi (π) establece la relación entre la longitud de la circunferencia y su diámetro. Anteriormente a este nombre, se le llamó constante de Arquímedes.


A lo largo de la historia, el número π ha sido objeto de numerosos matemáticos para determinar el valor de dicho númer. Algunas de las aproximaciones históricas realizadas son las que vamos a comentar:
  • EGIPTO: llevada a cabo por el egipcio Ahmes en el 1800 a.C. Según afirmaba, "el área del círculo es aproximadamente igual a la de un cuadrado de lado igual a 8/9 del diámetro del círculo".
                                      π= (8/9 d)² = 64/81 d² = 64/81 (4r²) = 256/81 = 3,16049...




  • MESOPOTAMIA: los matemáticos mesopotámicos empleaban para el cálculo de segmentos un valor de π igual a 3 + 1/8

  • MATEMÁTICA CHINA:  hacia el año 263, el matemático chino Liu Hui fue el primero en sugerir que 3,14 era una buena aproximación para π. Para descubrirlo, utilizó poligonos de 96 y 192 lados respectivamente. Posteriormente, estimó un valor de π igual a 3,14159 utilizando un políogono de 3.072 lados.



A pesar de ser un número irracional, es uno de los números más usados sobre todo en las siguientes materias: geometría, probabilidad, análisis matemático....


CURIOSIDADES DEL NÚMERO PI:

Para recordar las 20 primeras cifras del número π existe un poema, que contando las letras de cada palabra, coincide con los dígitos del número:

Soy y seré a todos definible
mi nombre tengo que daros
cociente diametral siempre inmedible
soy de los redondos aros 
No hay comentarios:

15 feb 2011

PARADOJAS DE ZENÓN DE ELEA

Las paradojas de Zenón de Elea son una serie de aporías para apoyar la doctrina de Parménides de que las sensaciones no son más que ilusiones, y con lo que intenta explicar que no existe el movimiento.
Las tres paradojas más conocidas de este filósofo griego son las siguientes:

AQUILES Y LA TORTUGA:
 Aquiles, un gran guerrero llamado el "pies ligero" decide salir a competir en una carrera contra una tortuga. Ya que corre mucho más rápido que la tortuga y seguro de sus posibilidades, le cede una gran ventaja inicial. Al darse la salida, Aquiles recorre la distancia que les separaba rápidamente, pero al llegar se da cuenta de que la tortuga no está ahí, sino que ha avanzado. Sigue corriendo, pero al llegar de nuevo a donde estaba la tortuga, ésta ha vuelto a avanzar.
Según lo anteriormente dicho, Aquiles no podrá ganar nunca la carrera, ya que para alcanzar a la tortuga, tendrá que recorrer un número infinito de puntos antes de alcanzarla.

LA DICOTOMÍA:
Esta paradoja es muy parecida a la anterior. Zenón se encuentra a ocho metros de un árbol. Llegado un momento, lanza una piedra, tratando de dar al árbol. La piedra antes de llegar al objetivo, primero ha de recorrer la mitad de la distancia que lo separa, es decir, los cuatro primeros metros. Después deberá recorrer esos cuatro metros restantes, pero para ello, de nuevo deberá recorrer la mitad de esa distancia. Según esta regla, siempre deberá recorrer la mitad de la distancia, por lo que la piedra nunca llegará al árbol.


LA PARADOJA DE LA FLECHA:
 
En esta paradoja, se lanza una flecha. En cada momento, la flecha está en una posición específica, y si ese momento es o suficientemente pequeño, la flecha no tiene tiempo para moverse, por lo que está en reposo durante ese instante. Ahora bien, durante los siguientes periodos de tiempo, la flecha también estará en reposo por el mismo motivo. De este modo, se puede llegar a la conclusión de que siempre está en reposo: el movimiento es imposible.



Estos son unos ejemplos, a través de los cuales Zenón intenta explicar que el movimiento físico no existe.
No hay comentarios:
Suscribirse a: Entradas (Atom)